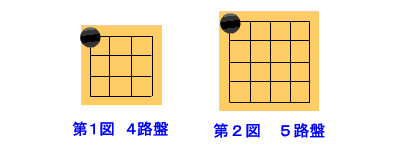
’０５年１１月１７日

　囲碁の手数の変化とコンピューターについて考えてみる。
簡単のために第１図、第２図のような碁盤について考察する。

１．４路盤の手数の変化
　第１図の４×４の盤では第１手目に黒石を置くことが出来る場所は１６ヶ所。次に第２手目の白石を置くことが出来るのは最初に黒が置いた場所を除いた１５ヶ所である。したがって第２手目までの黒石と白石を置く手数の変化の数は　１６×１５＝２４０　通りあることになる。
　
　このようにして、第３手目に黒石を置くことが出来る場所は１３ヶ所、第４手目の白石の場所は１２ヶ所と、手数が進むにつれて石を置くことの出来る場所が１ヶ所ずつ減少し、最後の１６手目には白石を置く場所は一つしかないことになる。

　第３手目までの手数の変化は　１６×１５×１４＝３，３６０　通り
　第４手目までの手数の変化は　１６×１５×１４×１３＝４３，６８０　通りである。

　以下　１６×１５×１４×１３×１２×・・・・・・・・・・×３×２×１　となり、これは
１６！（１６の階乗）ということになる。これを計算してみると
１６！（１６の階乗）＝２０，９２２，７８９，８８８，０００　（２０兆９２２７億８９８８万８千）
という値が得られる。

２．５路盤の手数の変化
　１項と同じように考えれば第２図の５×５の盤の手数の変化の数は　２５！（２５の階乗）となるが、この階乗値を計算するとなると途端に気力がなくなってしまったので、概算値だけを示すとその値は約１６（じょ）となる。

　（じょ）という漢字は　ＪＩＳ　の標準漢字表にはない字で（禾偏に予）と書き、

　一、十、千、万、億、兆、京（けい）、垓（がい）の一つ上位の桁のことである。

　この桁のところは（し）という漢字（この漢字も　ＪＩＳ　にはなく、偏は”禾”だが”つくり”の字がないので表現することが出来ない）をあてることもある。

　以上のことから碁盤の縦横の線が夫々１本増えるごとに変化の手数が飛躍的に大きくなることが予想され、１９×１９＝３６１階乗の値（３６１！）が前回述べたような天文学的な値以上（囲碁について（３））になることが理解出来るのである。

　次回はこれらの変化の手数をコンピューターで調べたらどの位の時間がかかるかについて考えてみる。
　
　　　　　’０５年１１月１８日
　現在のパソコンでは２Ｇないし３Ｇ位の周波数（クロック）のＣＰＵが使われているが、これらのＣＰＵのニーモニックが分からないので、ＭＳ−ＤＯＳ時代のＺ−８０（ＣＰＵ）の場合で計算し、それを元に推定することにする。

　ＣＰＵの周波数をＦとすると、その逆数　１/Ｆ　をクロックサイクルという。Ｚ−８０の場合、その周波数は最高でも　１０Ｍｈｚ　であるから、クロックサイクルの値は　１/（１０の７乗）＝０．１μｓ（千万分の１秒）となる。

　今、碁盤上に碁石が置かれているかいないかを調べるとすると、例えば碁盤上に石がある状態を　”１”　、石がない状態を　”０”　として、そのデータを予めコンピューターのメモリーに入れておき、そのメモリーの状態を調べるニーモニックは最も単純に考えた場合、

　ＬＤ　　Ａ，（ＨＬ）　：メモリー番地にあるデータ（碁盤上に石があるかないか）をＡレジスタに代　　　　　　　　　　　　　入
　ＪＰ　　Ｚ，○○○○　：Ａレジスタのデータを判定して、次の処理を行う　〇〇〇〇番地へジャンプ　　　　　　　　　　　　　する
としてよいであろう。

　上記の場合のニーモニックのクロックサイクルは夫々　”７”、”１０”であるが、両方で　”２０”とする。

　したがって盤上の1ヶ所を調べるのに要する時間は０．１×２０＝２μｓ（２百万分の１秒）になり、

（１）　４×４の盤上の石の有無を調べる時間は　（２０兆９２２７億８９８８万８千）×２百万分の１秒
　となる。この結果は概略4200万秒、時間に直すと約１１，１１１時間である。

　以上の結果を現在使用されているパソコンに適用する。

　３ＧのＣＰＵは３２ビットであるから８ビットのＺ−８０に比べて4倍のスピードがあるとし、クロックサイクルは３００倍速いから、両方で１２００倍のスピードということになる。

　したがって3Ｇパソコンでの処理時間は　１１，１１１÷１２００＝約９．３時間　ということにる。

（２）　次に　５×５の盤の場合はどうなるかであるが、考えるだけで気が重くなる。
　手数の変化は　４路盤に比べて
　（１６×（１０の２４乗））÷（２１×（１０の１２乗））＝約　８×（１０の１１乗）倍
多いから、必要な時間は
　９．３×８×（１０の１１乗）＝約７４×（１０の１１乗）時間
ということになる。日数に換算すると約　３×（１０の１１乗）日、即ち約８億年という途方もない時間になる。

　たった２５ケ所の石の有無の調査に８億年もかかるということなど、計算違いではないかと俄かには信じ難いが、何度考え直してもこういうことになる。

　根気と暇のある方がおられたら是非確認してみて下さい。